Pembahasan berikutnya tentang
osilator harmonik yaitu mencari solusi eigen (nilai eigen dan fungsi eigen).
Solusi eigen dibahas pada mata kuliah fisika kuantum. Ada beberapa metode untuk
mencari solusi eigen antara lain; mekanika matriks Heisenberg, persamaan
gelombang Schrodinger, dan metode integral jejak. Tiap metode mempunyai
kerumitannya masing-masing jadi pemilihan tergantung dari selera J
dan pada kesempatan ini metode yang digunakan adalah persamaan gelombang Schrodinger.
dimana V(x) adalah
energi potensial. Jadi bentuk persamaan Schrodinger untuk osilator harmonik
adalah :
Misalkan
maka persamaan awal akan menyusut menjadi :
untuk z → ∞ maka suku α/β dapat diabaikan sehingga didapat bentuk asimtotik
dengan solusi :
dari solusi tersebut
jika dimasukkan kembali ke persamaan yang telah disusutkan maka :
sehingga untuk q = 0 maka akan didapatkan
agar semua suku memperoleh pangkat yang sama dalm z maka dikenakan variasi indeks berjalan r sehingga diperoleh :
atau
Rumus rekursi di atas
mengisyaratkan bahwa ekspansi deret akan berhingga dan berhenti pada r = n jika
[2n + 1 – (α/β)] = 0, atau α/β = 2n+1. Dengan mensubtitusi kembali α dan β pada
pemisalan awal maka didapatkan :
dimana En disebut dengan nilai eigen
dimana En disebut dengan nilai eigen
Untuk harga α/β = 2n+1 maka persamaan diferensial untuk H berubah menjadi :
Bentuk
persamaan tersebut tidak lain adalah persamaan diferensial Hermite. Salah satu
cara menyelesaikan persamaan tersebut yaitu menggunakan fungsi pembangkit dari PD
fungsi Hermite yang dinyatakan sebagai :
Dengan demikian solusi
untuk persamaan awal U(x) atau fungsi eigen adalah :
Pentingnya osilator harmonik dalam fisika klasik maupun modern tidak terletak pada persyaratan ketat bahwa gaya pemulih yang sebenarnya memenuhi hukum Hooke yang jarang dijumpai, tetapi pada kenyataan bahwa gaya pemulihnya tereduksi agar memnuhi hukum Hooke untuk pergeseran yang kecil. Sebagai hasilnya, setiap sistem yang melakukan getaran kecil terhadap kedudukan setimbangnya berperilaku seperti osilator harmonik sederhana. Contohnya sebuah atom dalam kisi kristal atau vibrasi molekul dwiatom.
Pada beberapa buku
teks, konsep penyelesaian persamaan Schrodinger untuk osilator harmonik mungkin
berbeda, namun solusi eigen akan selalu sama. Hal yang ditekankan pada osilator
harmonik ini adalah :
1. Terdapat harga minimum untuk energi terendah yang diizinkan, E0.
2. Energi bersifat diskrit dengan harga tertentu saja.
Referensi :
1. Catatan
kuliah Fisika Kuantum oleh Prof.Dr.rer-nat. Wira Bahari Nurdin
2. “Pengantar
Fisika Kuantum” (Agus Purwanto)
3. “Konsep
Fisika Modern” (Arthur Beiser)

















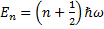





0 komentar:
Posting Komentar