Gerak harmonik sederhana adalah
gerak bolak-balik benda melalui suatu titik kesetimbangan tertentu dengan
banyaknya getaran benda dalam setiap sekon selalu konstan. Gerak harmonik
terjadi jika suatu sistem jenis tertentu bergetar di sekitar konfigurasi setimbangnya.
Persyaratan supaya gerak harmonik terjadi adalah terdapatnya gaya pemulih yang
beraksi untuk mengembalikan ke konfigurasi setimbangnya jika sistem tersebut
diganggu. Semua osilasi mempunyai karakter harmonik sederhana jika amplitudonya
cukup kecil. Contoh gerak harmonik sederhana yaitu gerak pada pegas dan bandul.
a. Pegas
Gerak harmonik terjadi pada pegas dengan konstanta pegas k
jika pada pegas tersebut diberikan beban sebesar m. Jika beban pada pegas
tersebut ditarik (diberi simpangan), maka akan terjadi gerak osilasi.
Gaya
pemulih yang bekerja pada pegas adalah F = -k x, dengan k adalah konstanta
pegas dan x adalah perubahan panjang pada pegas. Tanda negatif (-) menyatakan
bahwa aksi gaya F selalu berlawanan dengan reaksi pegas kx.
Gaya pemulih pada pegas ini dikenal sebagai “Hukum Hooke”.
Periode dan frekuensi pada pegas dapat dicari dengan memasukkan Hukum Hooke ke
dalam Hukum Kedua Newton
Dari hubungan di atas maka frekuensi (f) dan periode (T) sistem dapat ditentukan.
b. Bandul Sederhana
Bandul sederhana adalah
benda ideal yang terdiri dari sebuah titik massa yang digantungkan pada tali
ringan (massa tali diabaikan). Jika bandul ditarik ke samping dari posisi
setimbang dan dilepas, maka bandul akan berayun dalam bidang vertikal karena
pengaruh gravitasi. Geraknya merupakan gerak osilasi dan periodik
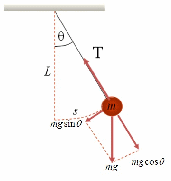
Tinjau gaya-gaya pada massa m.
dalam arah vertical, massa m dipengaruhi oleh gaya beratnya yaitu sebesar w =
mg. Gaya berat tersebut memiliki komponen sumbu x sebesar mg sin θ dan komponen
sumbu y sebesar mg cos θ.
Dalam arah sumbu y, komponen gaya
berat diimbangi oleh tegangan tali T sehingga gaya dalam arah sumbu y bernilai
nol. Gaya dalam arah sumbu x merupakan gaya pemulih, yaitu gaya yang selalu
menuju titik keseimbangan. Arah gaya tersebut berlawanan arah dengan simpangan,
sehingga dapat ditulis :
F = - mg sin θ, sin θ = x/L
Dari gaya pemulih
tersebut maka periode dan frekuensi sistem dapat dicari
Percepatan gravitasi dapat dicari pada bandul sederhana ini dengan rumus :
Oleh karena itu pada
percobaan bandul matematis tujuan yang ingin dicapai adalah menentukan atau
membuktikan nilai percepatan gravitasi (g = 9,8 m/s2).
Referensi :
- Catatan kuliah “Fiska Gelombang Mekanik” oleh Drs. Arsyad Sumah
- Penuntun Praktikum Fiska Dasar II TA 2005-2006. UPT MKU Univ. Hasanuddin
- http://id.wikipedia.org/wiki/Berkas:Simple_Harmonic_Motion_Orbit.gif (picture pegas)
- http://dc407.4shared.com/doc/QIVDqj0h/preview_html_1abc19c8.gif (picture bandul)
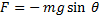
0 komentar:
Posting Komentar